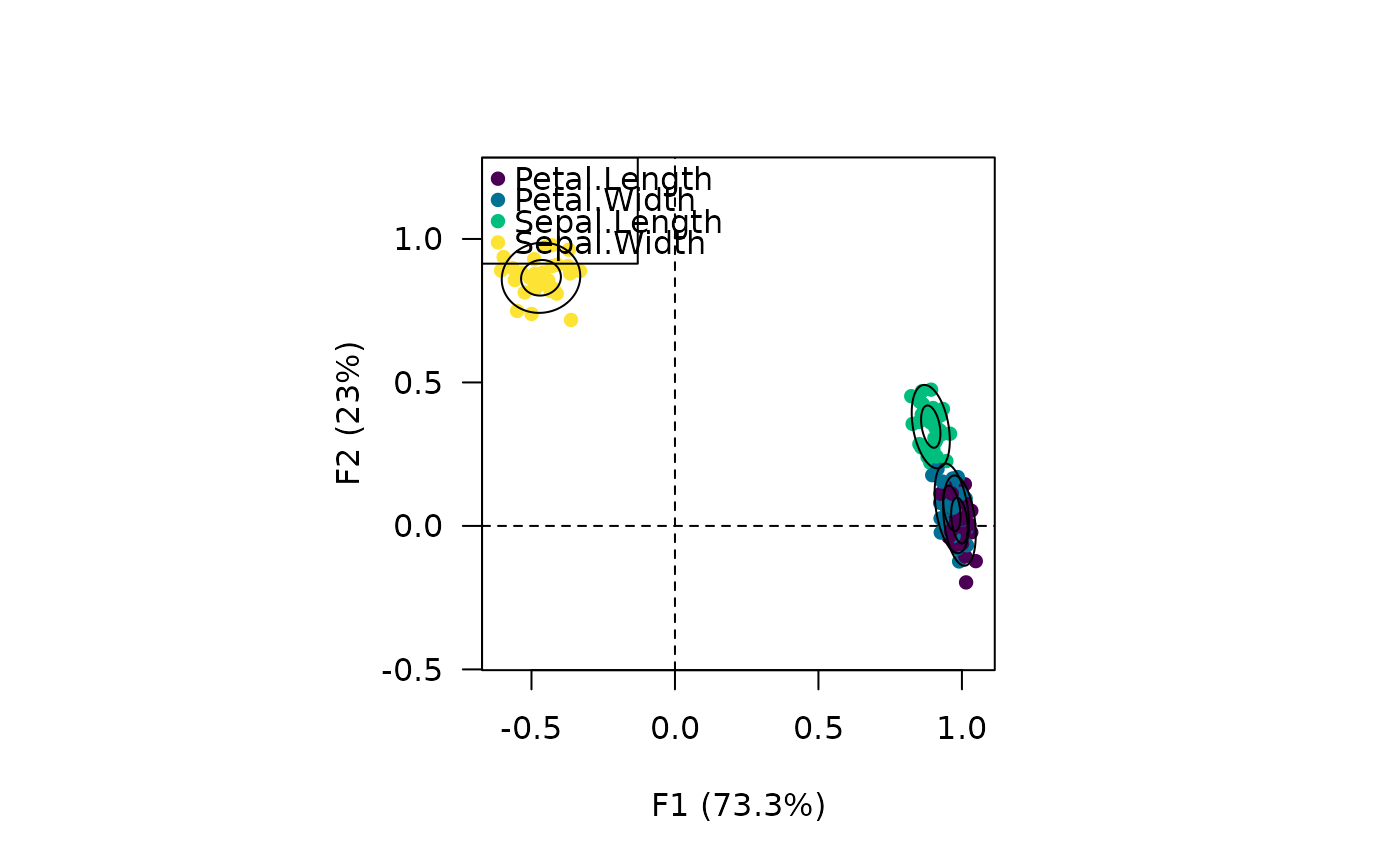Checks analysis with partial bootstrap resampling.
Usage
# S4 method for class 'CA'
bootstrap(object, n = 30)
# S4 method for class 'PCA'
bootstrap(object, n = 30)Value
Returns a BootstrapCA or a BootstrapPCA object.
References
Greenacre, Michael J. Theory and Applications of Correspondence Analysis. London: Academic Press, 1984.
Lebart, L., Piron, M. and Morineau, A. Statistique exploratoire multidimensionnelle: visualisation et inférence en fouille de données. Paris: Dunod, 2006.
Lockyear, K. (2013). Applying Bootstrapped Correspondence Analysis to Archaeological Data. Journal of Archaeological Science, 40(12): 4744-4753. doi:10.1016/j.jas.2012.08.035 .
Ringrose, T. J. (1992). Bootstrapping and Correspondence Analysis in Archaeology. Journal of Archaeological Science, 19(6): 615-629. doi:10.1016/0305-4403(92)90032-X .
Examples
## Bootstrap on CA
## Data from Lebart et al. 2006, p. 170-172
data("colours")
## Compute correspondence analysis
X <- ca(colours)
## Bootstrap (30 replicates)
Y <- bootstrap(X, n = 30)
if (FALSE) { # \dontrun{
## Get replicated coordinates
get_replications(Y, margin = 1)
get_replications(Y, margin = 2)
} # }
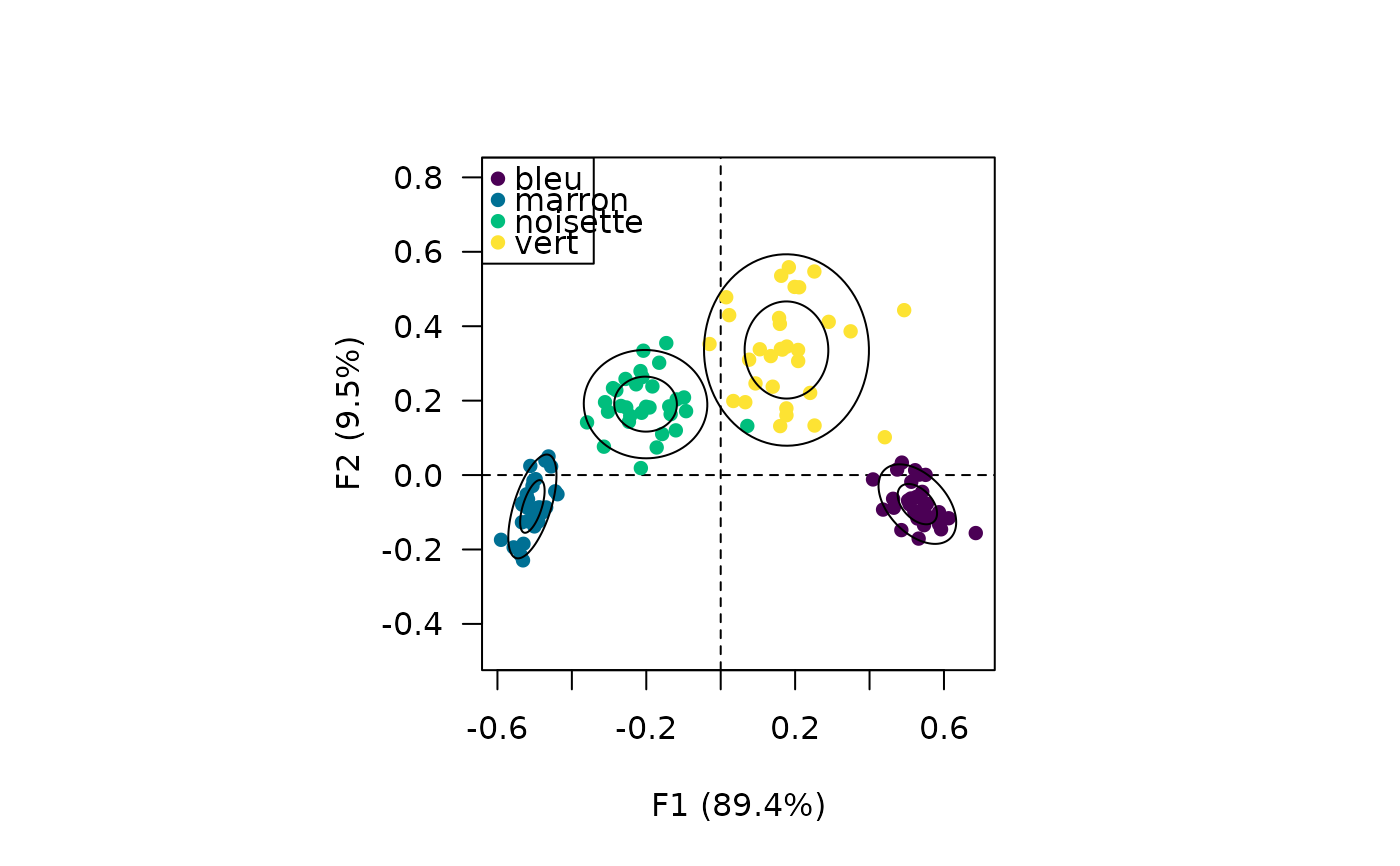
## Plot with ellipses
viz_rows(Y)
viz_tolerance(Y, level = c(0.68, 0.95))
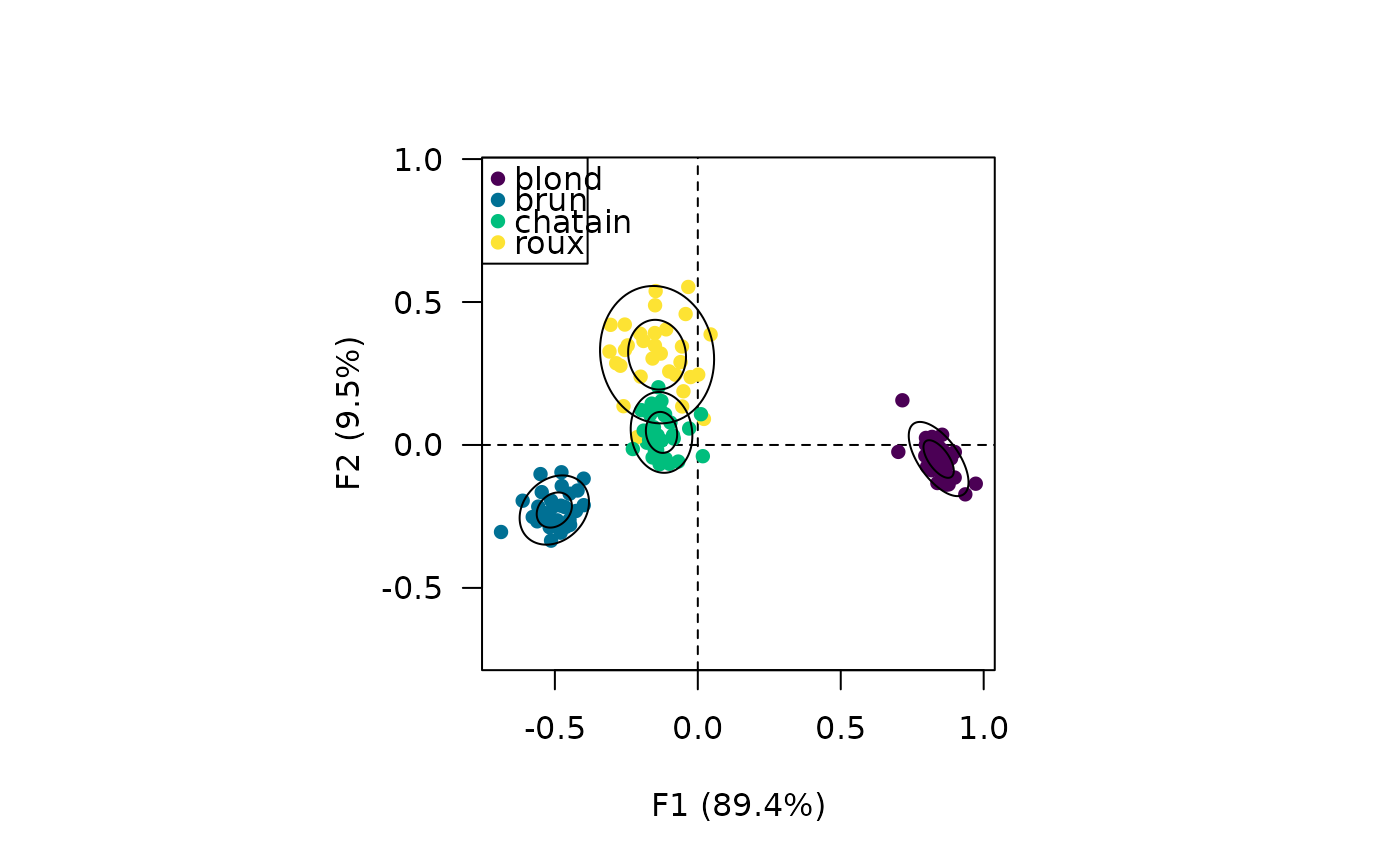
 viz_columns(Y)
viz_tolerance(Y, level = c(0.68, 0.95))
viz_columns(Y)
viz_tolerance(Y, level = c(0.68, 0.95))
 ## Plot with convex hulls
viz_columns(Y)
viz_hull(Y)
## Plot with convex hulls
viz_columns(Y)
viz_hull(Y)
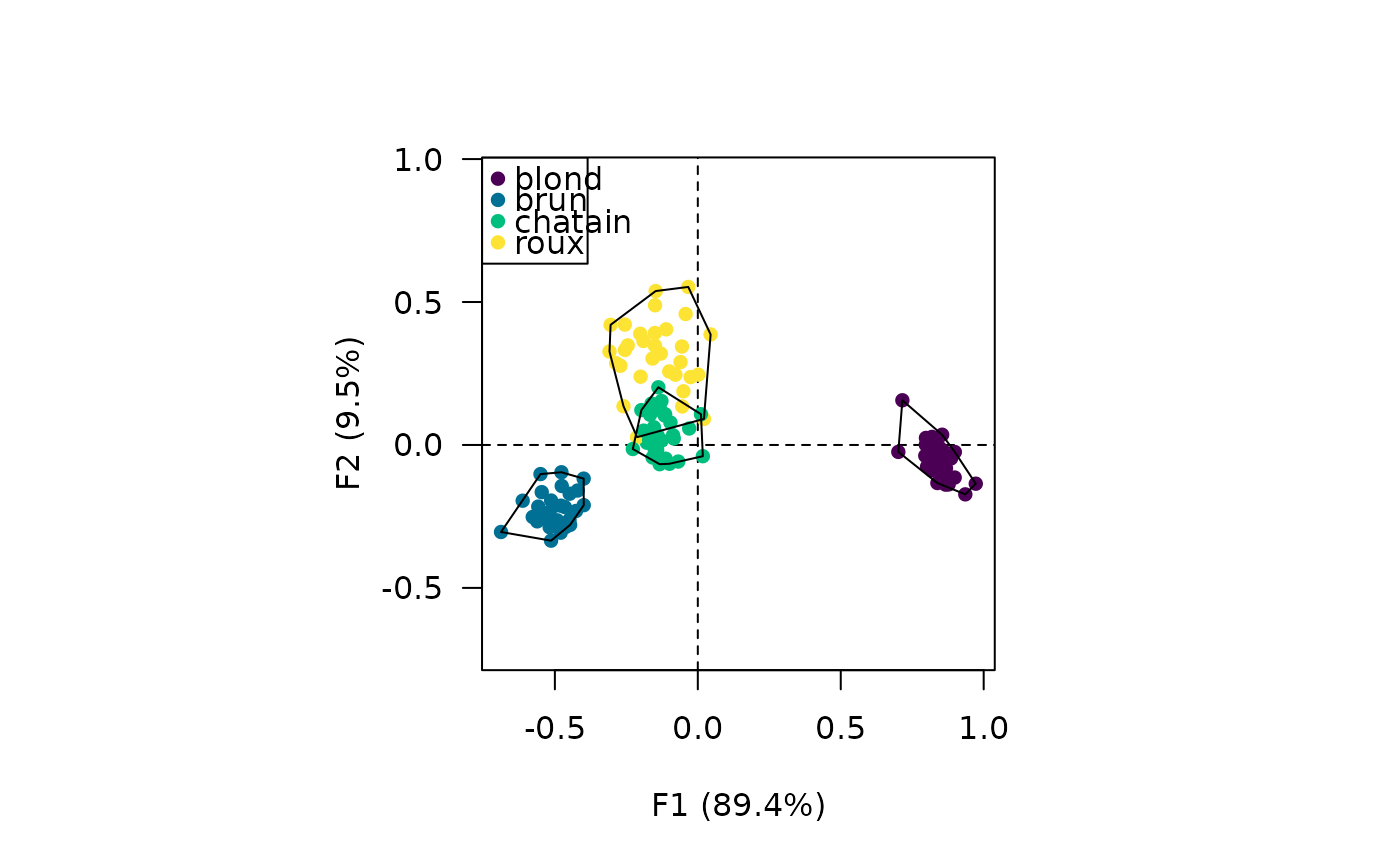 ## Bootstrap on PCA
## Compute principal components analysis
data("iris")
X <- pca(iris, sup_quali = "Species")
## Bootstrap (30 replicates)
Y <- bootstrap(X, n = 30)
## Plot with ellipses
viz_variables(Y)
viz_tolerance(Y, level = c(0.68, 0.95))
## Bootstrap on PCA
## Compute principal components analysis
data("iris")
X <- pca(iris, sup_quali = "Species")
## Bootstrap (30 replicates)
Y <- bootstrap(X, n = 30)
## Plot with ellipses
viz_variables(Y)
viz_tolerance(Y, level = c(0.68, 0.95))