Event Date Model

## Install extra packages (if needed):
# install.packages("folio") # datasets

# Load packages
library(kairos)
#> Loading required package: dimensio

Definition

Event and accumulation dates are density estimates of the occupation and duration of an archaeological site (Bellanger, Husi and Tomassone 2006; Bellanger, Tomassone and Husi 2008; Bellanger and Husi 2012).

The event date is an estimation of the terminus post-quem of an archaeological assemblage. The accumulation date represents the “chronological profile” of the assemblage. According to Bellanger and Husi (2012), accumulation date can be interpreted “at best […] as a formation process reflecting the duration or succession of events on the scale of archaeological time, and at worst, as imprecise dating due to contamination of the context by residual or intrusive material.” In other words, accumulation dates estimate occurrence of archaeological events and rhythms of the long term.

Event Date

Event dates are estimated by fitting a Gaussian multiple linear regression model on the factors resulting from a correspondence analysis - somewhat similar to the idea introduced by Poblome and Groenen (2003). This model results from the known dates of a selection of reliable contexts and allows to predict the event dates of the remaining assemblages.

First, a correspondence analysis (CA) is carried out to summarize the information in the count matrix $X$ . The correspondence analysis of $X$ provides the coordinates of the $m$ rows along the $q$ factorial components, denoted $f_{ik} ~\forall i \in \left[ 1,m \right], k \in \left[ 1,q \right]$ .

Then, assuming that $n$ assemblages are reliably dated by another source, a Gaussian multiple linear regression model is fitted on the factorial components for the $n$ dated assemblages:

$t^E_i = \beta_{0} + \sum_{k = 1}^{q} \beta_{k} f_{ik} + \epsilon_i ~\forall i \in [1,n]$ where $t^E_i$ is the known date point estimate of the $i$ th assemblage, $\beta_k$ are the regression coefficients and $\epsilon_i$ are normally, identically and independently distributed random variables, $\epsilon_i \sim \mathcal{N}(0,\sigma^2)$ .

These $n$ equations are stacked together and written in matrix notation as

$t^E = F \beta + \epsilon$

where $\epsilon \sim \mathcal{N}_{n}(0,\sigma^2 I_{n})$ , $\beta = \left[ \beta_0 \cdots \beta_q \right]' \in \mathbb{R}^{q+1}$ and

$F = \begin{bmatrix} 1 & f_{11} & \cdots & f_{1q} \\ 1 & f_{21} & \cdots & f_{2q} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & f_{n1} & \cdots & f_{nq} \end{bmatrix}$

Assuming that $F'F$ is nonsingular, the ordinary least squares estimator of the unknown parameter vector $\beta$ is:

$\widehat{\beta} = \left( F'F \right)^{-1} F' t^E$

Finally, for a given vector of CA coordinates $f_i$ , the predicted event date of an assemblage $t^E_i$ is:

$\widehat{t^E_i} = f_i \hat{\beta}$

The endpoints of the $100(1 − \alpha)$ % associated prediction confidence interval are given as:

$\widehat{t^E_i} \pm t_{\alpha/2,n-q-1} \sqrt{\widehat{V}}$

where $\widehat{V_i}$ is an estimator of the variance of the prediction error: $\widehat{V_i} = \widehat{\sigma}^2 \left( f_i^T \left( F'F \right)^{-1} f_i + 1 \right)$

were $\widehat{\sigma} = \frac{\sum_{i=1}^{n} \left( t_i - \widehat{t^E_i} \right)^2}{n - q - 1}$ .

The probability density of an event date $t^E_i$ can be described as a normal distribution:

$t^E_i \sim \mathcal{N}(\widehat{t^E_i},\widehat{V_i})$

Accumulation Date

As row (assemblages) and columns (types) CA coordinates are linked together through the so-called transition formulae, event dates for each type $t^E_j$ can be predicted following the same procedure as above.

Then, the accumulation date $t^A_i$ is defined as the weighted mean of the event date of the ceramic types found in a given assemblage. The weights are the conditional frequencies of the respective types in the assemblage (akin to the MCD).

The accumulation date is estimated as: $\widehat{t^A_i} = \sum_{j = 1}^{p} \widehat{t^E_j} \times \frac{x_{ij}}{x_{i \cdot}}$

The probability density of an accumulation date $t^A_i$ can be described as a Gaussian mixture:

$t^A_i \sim \frac{x_{ij}}{x_{i \cdot}} \mathcal{N}(\widehat{t^E_j},\widehat{V_j}^2)$

Interestingly, the integral of the accumulation date offers an estimates of the cumulative occurrence of archaeological events, which is close enough to the definition of the tempo plot introduced by Dye (2016).

Limitation

Event and accumulation dates estimation relies on the same conditions and assumptions as the matrix seriation problem. Dunnell (1970) summarizes these conditions and assumptions as follows.

The homogeneity conditions state that all the groups included in a seriation must:

Be of comparable duration.
Belong to the same cultural tradition.
Come from the same local area.

The mathematical assumptions state that the distribution of any historical or temporal class:

Is continuous through time.
Exhibits the form of a unimodal curve.

Theses assumptions create a distributional model and ordering is accomplished by arranging the matrix so that the class distributions approximate the required pattern. The resulting order is inferred to be chronological.

Predicted dates have to be interpreted with care: these dates are highly dependent on the range of the known dates and the fit of the regression.

Usage

This package provides an implementation of the chronological modeling method developed by Bellanger and Husi (2012). This method is slightly modified here and allows the construction of different probability density curves of archaeological assemblage dates (event, activity and tempo).

## Bellanger et al. did not publish the data supporting their demonstration: 
## no replication of their results is possible. 
## Here is an example using the Zuni dataset from Peeples and Schachner 2012
data("zuni", package = "folio")

## Assume that some assemblages are reliably dated (this is NOT a real example)
## The names of the vector entries must match the names of the assemblages
zuni_dates <- c(
  LZ0569 = 1097, LZ0279 = 1119, CS16 = 1328, LZ0066 = 1111,
  LZ0852 = 1216, LZ1209 = 1251, CS144 = 1262, LZ0563 = 1206,
  LZ0329 = 1076, LZ0005Q = 859, LZ0322 = 1109, LZ0067 = 863,
  LZ0578 = 1180, LZ0227 = 1104, LZ0610 = 1074
)

## Model the event and accumulation date for each assemblage
model <- event(zuni, dates = zuni_dates, rank = 10)

## Extract model coefficients
## (convert results to Gregorian years)
coef(model, calendar = CE())
#>  (Intercept)           F1           F2           F3           F4           F5 
#> 1163.6525183 -158.2876592   25.7026078   -5.6049778   10.7570247   -3.1382078 
#>           F6           F7           F8           F9          F10 
#>    2.7245577    4.5641627   11.2966954   -5.1721456   -0.3965122

## Extract residual standard deviation
## (convert results to Gregorian years)
sigma(model, calendar = CE())
#> [1] 4.090834

## Extract model residuals
## (convert results to Gregorian years)
resid(model, calendar = CE())
#>     LZ0852     LZ0610     LZ0578     LZ0569     LZ0563     LZ0329     LZ0322 
#> -1.3123347  0.9623218  3.5141430  0.4478299 -4.4537670 -0.7964654  2.6011154 
#>     LZ0279     LZ0227     LZ0067     LZ0066    LZ0005Q       CS16      CS144 
#> -3.9079020 -0.7682236 -0.1375450  0.7283483  0.1254681 -0.2887566  2.7823817 
#>     LZ1209 
#>  0.5033862

## Extract model fitted values
## (convert results to Gregorian years)
fitted(model, calendar = CE())
#>  [1] 1217.3105 1073.0370 1176.4849 1096.5531 1210.4540 1076.7948 1106.3999
#>  [8] 1122.9078 1104.7666  863.1376 1110.2712  858.8744 1328.2882 1259.2185
#> [15] 1250.4963

## Estimate event dates
eve <- predict_event(model, margin = 1, level = 0.95)
head(eve)
#>             date     lower     upper    error
#> LZ1105 1168.5901 1152.1407 1185.0396 6.923526
#> LZ1103 1143.1063 1136.3822 1149.8294 3.420707
#> LZ1100 1156.3091 1141.0492 1171.5681 6.494020
#> LZ1099 1098.8294 1086.9674 1110.6942 5.269872
#> LZ1097 1088.4302 1078.1029 1098.7571 4.717296
#> LZ1096  839.8136  824.5635  855.0621 6.490568

## Estimate accumulation dates (median)
acc <- predict_accumulation(model, level = 0.95)
head(acc)
#>             date     lower    upper
#> LZ1105 1172.1053 1089.4725 1237.140
#> LZ1103 1120.9272  776.5453 1285.652
#> LZ1100 1205.6884  951.9349 1251.002
#> LZ1099 1091.0728 1058.5542 1118.796
#> LZ1097 1093.2039  776.0133 1251.002
#> LZ1096  782.9428  770.6816 1118.796

## Activity plot
plot(model, type = "activity", event = TRUE, select = 1:6)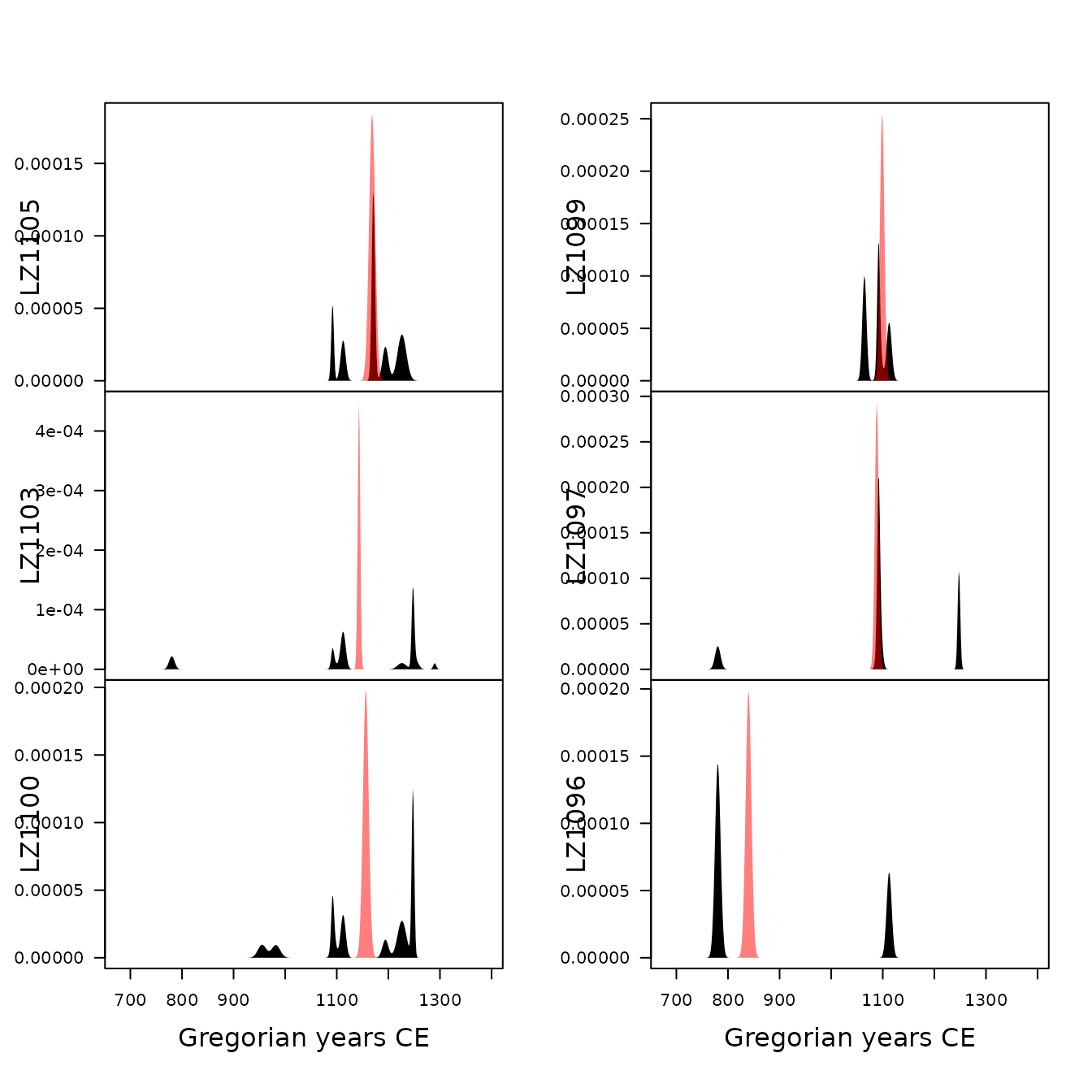

plot(model, type = "activity", event = TRUE, select = "LZ1105")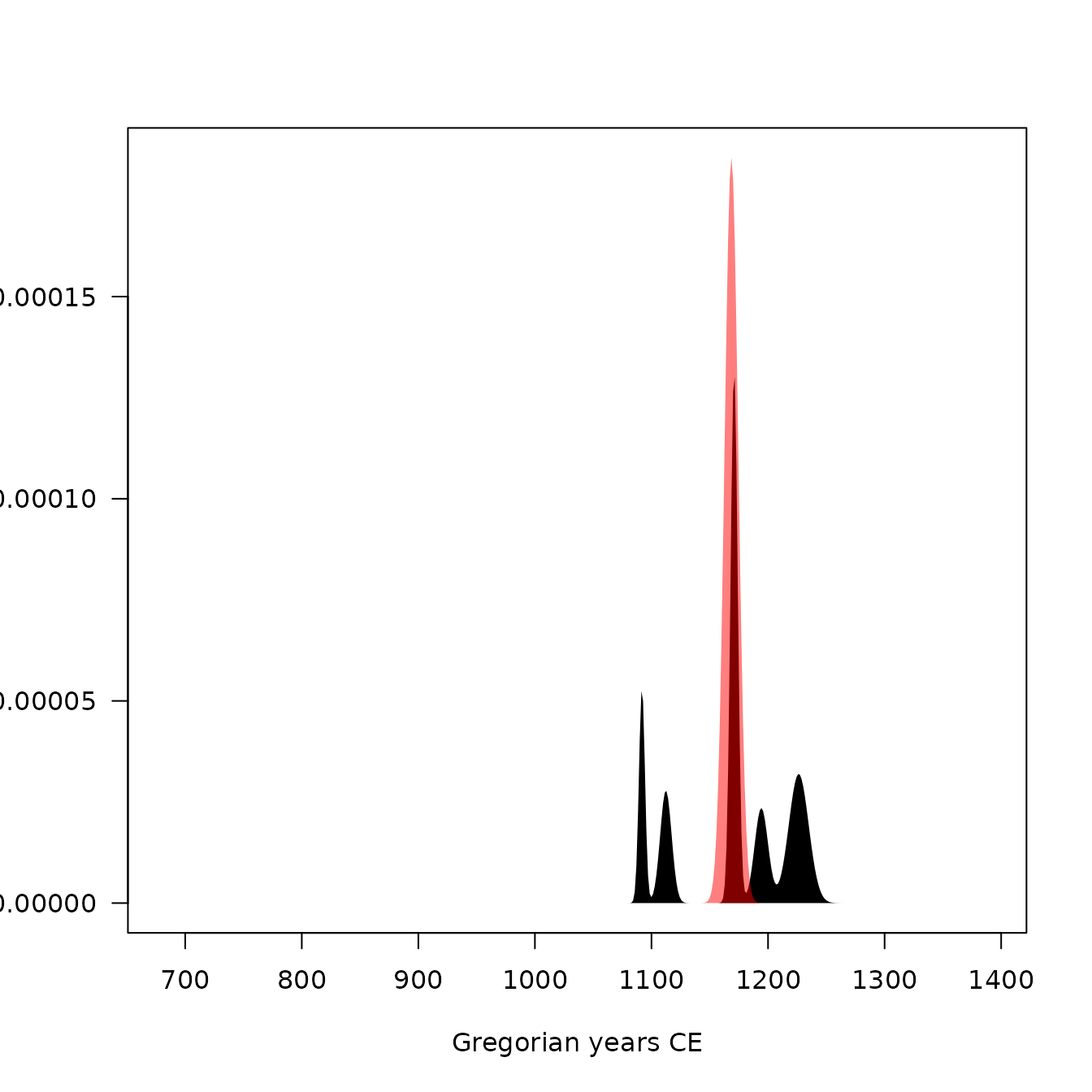


## Tempo plot
plot(model, type = "tempo", select = "LZ1105")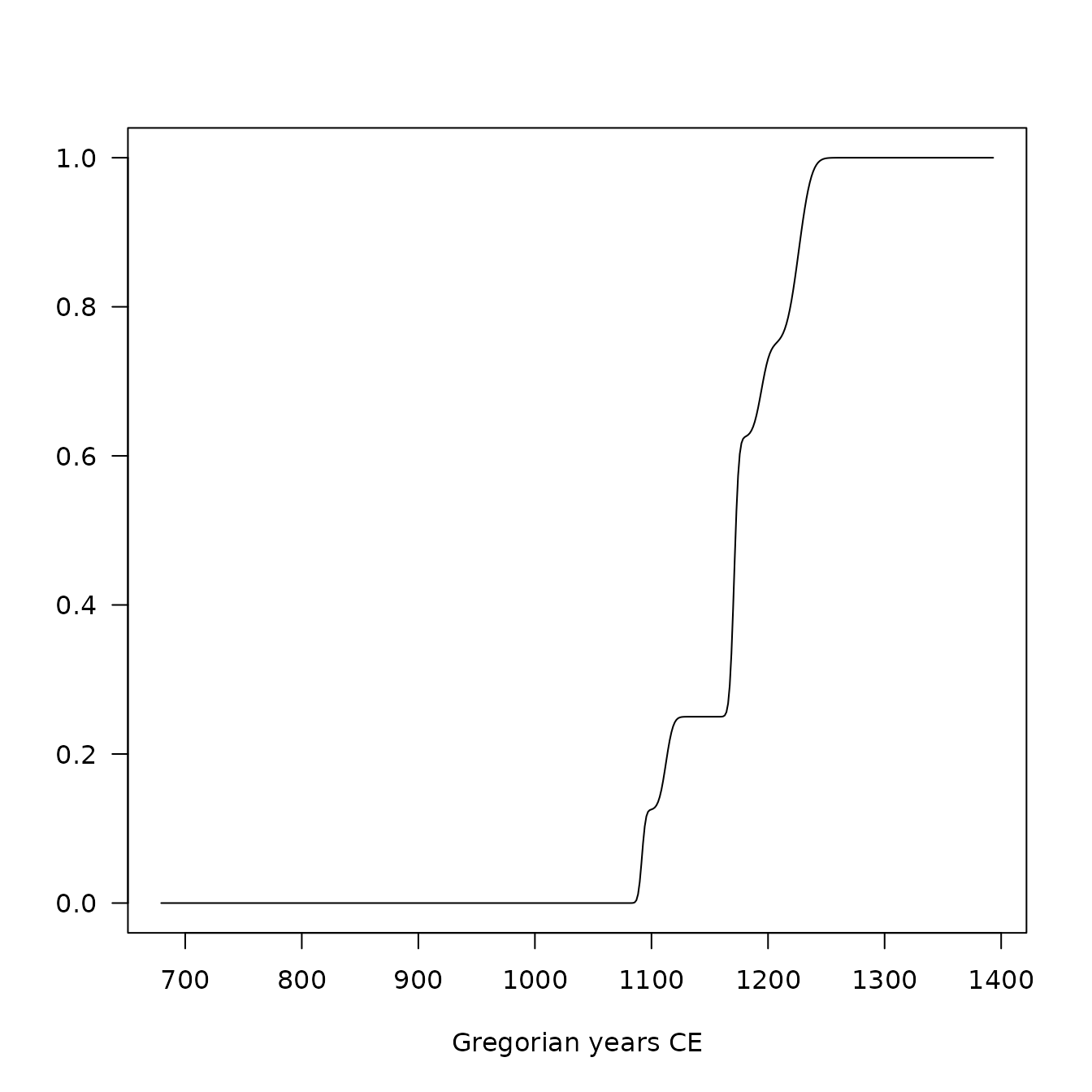

Resampling methods can be used to check the stability of the resulting model. If jackknife() is used, one type/fabric is removed at a time and all statistics are recalculated. In this way, one can assess whether certain type/fabric has a substantial influence on the date estimate. If bootstrap() is used, a large number of new bootstrap assemblages is created, with the same sample size, by resampling the original assemblage with replacement. Then, examination of the bootstrap statistics makes it possible to pinpoint assemblages that require further investigation.

## Check model variability
## Jackknife fabrics
jack <- jackknife(model)
head(jack)
#>             date     lower     upper
#> LZ1105 1035.1315 1018.6809 1051.5821
#> LZ1103 1280.8505 1274.1270 1287.5759
#> LZ1100 1120.9870 1105.7288 1136.2471
#> LZ1099 1028.1890 1016.3265 1040.0514
#> LZ1097  320.6905  310.3640  331.0181
#> LZ1096  769.9842  754.7357  785.2327

## Bootstrap of assemblages
boot <- bootstrap(model, n = 30)
head(boot)
#>              min      mean       max        Q5       Q95
#> LZ1105 1135.4879 1168.4161 1237.3648 1139.0678 1196.5042
#> LZ1103 1104.5113 1152.9632 1194.4472 1118.1088 1187.3170
#> LZ1100 1086.9757 1146.9817 1180.9436 1094.5631 1178.0472
#> LZ1099 1089.2295 1098.3497 1112.1438 1090.5814 1106.9976
#> LZ1097  998.2845 1082.5811 1176.2487 1008.3680 1152.8302
#> LZ1096  726.0654  827.0029  971.0624  726.0654  925.1247

References

Bellanger, L., Husi, P. & Tomassone, R. (2006). Une approche statistique pour la datation de contextes archéologiques. Revue de statistique appliquée, 54(2), 65-81. URL: http://www.numdam.org/item/RSA_2006__54_2_65_0/.

Bellanger, L. & Husi, P. (2012). Statistical Tool for Dating and Interpreting Archaeological Contexts Using Pottery. Journal of Archaeological Science, 39(4), 777-790. DOI: 10.1016/j.jas.2011.06.031.

Bellanger, L. & Tomassone, R. & Husi, P. (2008). A Statistical Approach for Dating Archaeological Contexts. Journal of Data Science, 6, 135-154.

Dunnell, R. C. (1970). Seriation Method and Its Evaluation. American Antiquity, 35(3), 305-319. DOI: 10.2307/278341.

Dye, T. S. (2016). Long-Term Rhythms in the Development of Hawaiian Social Stratification. Journal of Archaeological Science, 71, 1-9. DOI: 10.1016/j.jas.2016.05.006.

Poblome, J. & Groenen, P. J. F. (2003). Constrained Correspondence Analysis for Seriation of Sagalassos Tablewares. In M. Doerr & A. Sarris (Eds.), The Digital Heritage of Archaeology Athens: Hellenic Ministry of Culture.