Event and Accumulation Dates

Fits a date event model.

Usage

event(object, dates, ...)

# S4 method for data.frame,numeric
event(object, dates, rank = NULL, sup_row = NULL, calendar = CE(), ...)

# S4 method for matrix,numeric
event(object, dates, rank = NULL, sup_row = NULL, calendar = CE(), ...)

# S4 method for EventDate
summary(object, ...)

Arguments

object: A \(m \times p\) numeric matrix or data.frame of count data (absolute frequencies giving the number of individuals for each category, i.e. a contingency table). A data.frame will be coerced to a numeric matrix via data.matrix().
dates: A numeric vector of dates. If named, the names must match the row names of object.
...: Further arguments to be passed to internal methods.
rank: An integer specifying the number of CA factorial components to be use for linear model fitting (see details). If NULL (the default), axes corresponding to at least 60% of the inertia will be used.
sup_row: A numeric or logical vector specifying the indices of the supplementary rows.
calendar: A TimeScale object specifying the calendar of dates (see calendar()). Defaults to Gregorian Common Era.

Value

An EventDate object.

Details

This is an implementation of the chronological modeling method proposed by Bellanger and Husi (2012, 2013).

Event and accumulation dates are density estimates of the occupation and duration of an archaeological site (Bellanger and Husi 2012, 2013). The event date is an estimation of the terminus post-quem of an archaeological assemblage. The accumulation date represents the "chronological profile" of the assemblage. According to Bellanger and Husi (2012), accumulation date can be interpreted "at best [...] as a formation process reflecting the duration or succession of events on the scale of archaeological time, and at worst, as imprecise dating due to contamination of the context by residual or intrusive material." In other words, accumulation dates estimate occurrence of archaeological events and rhythms of the long term.

Dates are converted to rata die before any computation.

This method relies on strong archaeological and statistical assumptions (see vignette("event")).

References

Bellanger, L. & Husi, P. (2013). Mesurer et modéliser le temps inscrit dans la matière à partir d'une source matérielle : la céramique médiévale. In Mesure et Histoire Médiévale. Histoire ancienne et médiévale. Paris: Publication de la Sorbonne, p. 119-134.

Bellanger, L. & Husi, P. (2012). Statistical Tool for Dating and Interpreting Archaeological Contexts Using Pottery. Journal of Archaeological Science, 39(4), 777-790. doi:10.1016/j.jas.2011.06.031 .

Bellanger, L., Tomassone, R. & Husi, P. (2008). A Statistical Approach for Dating Archaeological Contexts. Journal of Data Science, 6, 135-154.

Bellanger, L., Husi, P. & Tomassone, R. (2006). Une approche statistique pour la datation de contextes archéologiques. Revue de Statistique Appliquée, 54(2), 65-81.

Bellanger, L., Husi, P. & Tomassone, R. (2006). Statistical Aspects of Pottery Quantification for the Dating of Some Archaeological Contexts. Archaeometry, 48(1), 169-183. doi:10.1111/j.1475-4754.2006.00249.x .

Poblome, J. & Groenen, P. J. F. (2003). Constrained Correspondence Analysis for Seriation of Sagalassos Tablewares. In Doerr, M. & Apostolis, S. (eds.), The Digital Heritage of Archaeology. Athens: Hellenic Ministry of Culture.

Author

N. Frerebeau

Examples

## Data from Peeples and Schachner 2012
data("zuni", package = "folio")

## Assume that some assemblages are reliably dated (this is NOT a real example)
zuni_dates <- c(
  LZ0569 = 1097, LZ0279 = 1119, CS16 = 1328, LZ0066 = 1111,
  LZ0852 = 1216, LZ1209 = 1251, CS144 = 1262, LZ0563 = 1206,
  LZ0329 = 1076, LZ0005Q = 859, LZ0322 = 1109, LZ0067 = 863,
  LZ0578 = 1180, LZ0227 = 1104, LZ0610 = 1074
)

## Model the event and accumulation date for each assemblage
model <- event(zuni, zuni_dates, rank = 10)
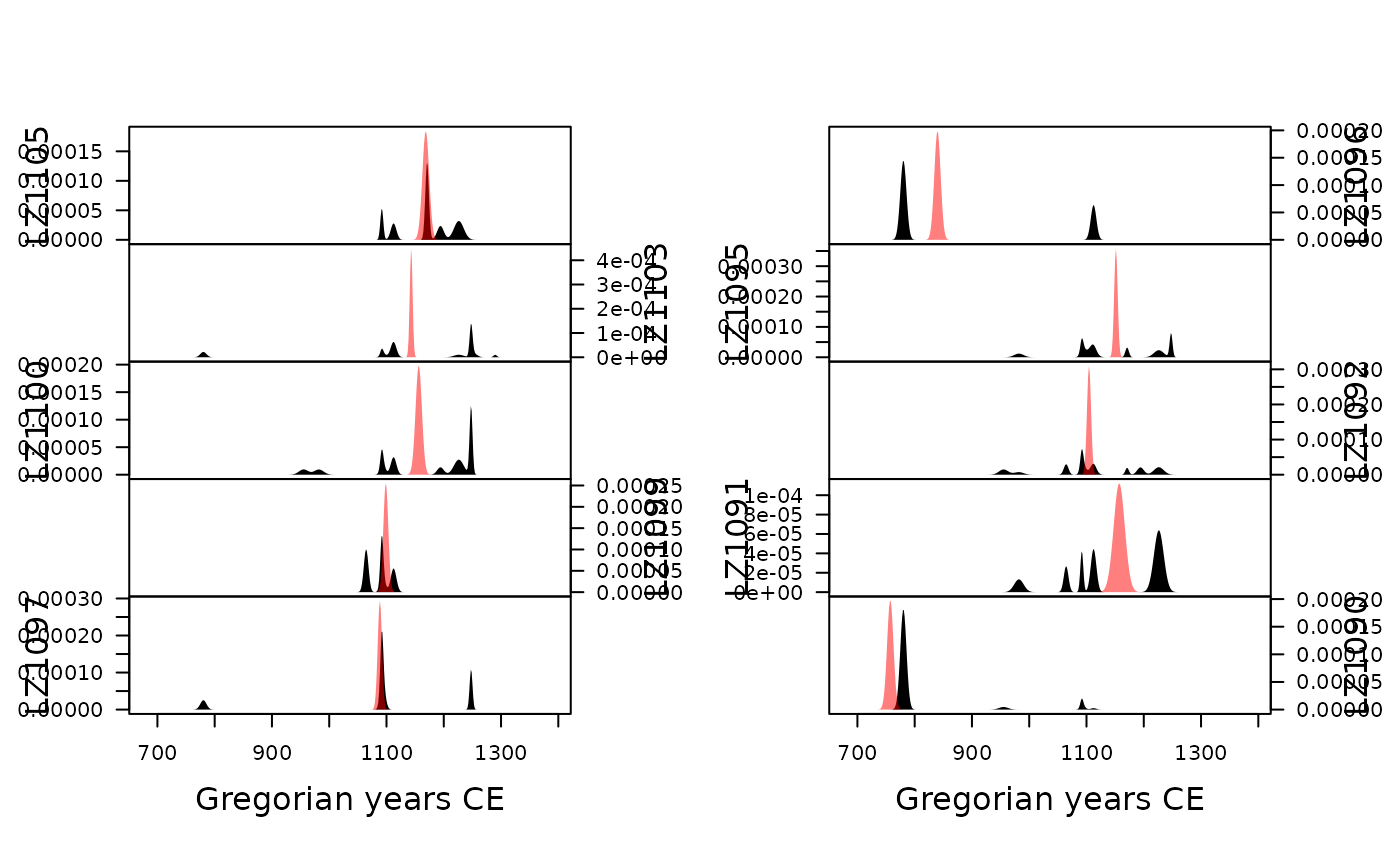
plot(model, select = 1:10, event = TRUE, flip = TRUE)