MCD Plot

MCD Plot

Usage

# S4 method for class 'MeanDate,missing'
plot(
  x,
  calendar = getOption("kairos.calendar"),
  decreasing = TRUE,
  main = NULL,
  sub = NULL,
  ann = graphics::par("ann"),
  axes = TRUE,
  frame.plot = axes,
  panel.first = NULL,
  panel.last = NULL,
  ...
)

# S4 method for class 'SimulationMeanDate,missing'
plot(
  x,
  calendar = getOption("kairos.calendar"),
  interval = "student",
  level = 0.8,
  decreasing = TRUE,
  main = NULL,
  sub = NULL,
  ann = graphics::par("ann"),
  axes = TRUE,
  frame.plot = axes,
  panel.first = NULL,
  panel.last = NULL,
  ...
)

Arguments

x: A MeanDate object.
calendar: An aion::TimeScale object specifying the target calendar (see calendar()).
decreasing: A logical scalar: should the sort be increasing or decreasing?
main: A character string giving a main title for the plot.
sub: A character string giving a subtitle for the plot.
ann: A logical scalar: should the default annotation (title and x, y and z axis labels) appear on the plot?
axes: A logical scalar: should axes be drawn on the plot?
frame.plot: A logical scalar: should a box be drawn around the plot?
panel.first: An an expression to be evaluated after the plot axes are set up but before any plotting takes place. This can be useful for drawing background grids.
panel.last: An expression to be evaluated after plotting has taken place but before the axes, title and box are added.
...: Further graphical parameters.
interval: A character string giving the type of confidence interval to be returned. It must be one "student" (the default), "normal", "percentiles" or "range" (min-max). Any unambiguous substring can be given.
level: A length-one numeric vector giving the confidence level. Only used if interval is not "range".

Value

plot() is called it for its side-effects: it results in a graphic being displayed (invisibly returns x).

Author

N. Frerebeau

Examples

## Data from Peeples and Schachner 2012
data("zuni", package = "folio")

## Set the start and end dates for each ceramic type
dates <- list(
  LINO = c(600, 875), KIAT = c(850, 950), RED = c(900, 1050),
  GALL = c(1025, 1125), ESC = c(1050, 1150), PUBW = c(1050, 1150),
  RES = c(1000, 1200), TULA = c(1175, 1300), PINE = c(1275, 1350),
  PUBR = c(1000, 1200), WING = c(1100, 1200), WIPO = c(1125, 1225),
  SJ = c(1200, 1300), LSJ = c(1250, 1300), SPR = c(1250, 1300),
  PINER = c(1275, 1325), HESH = c(1275, 1450), KWAK = c(1275, 1450)
)

## Calculate date midpoints
mid <- vapply(X = dates, FUN = mean, FUN.VALUE = numeric(1))

## Calculate MCD
(mc_dates <- mcd(zuni[100:125, ], dates = mid))
#> 26 x 18 x 1 time series observed between 276230.3 and 459613.1 r.d.

## Get MCD in years CE
time(mc_dates, calendar = CE())
#>  [1]  757.2912  796.6659  797.4991  952.5855  996.2952 1016.0738 1027.5011
#>  [8] 1059.5249 1073.6597 1075.5213 1089.5820 1092.8564 1100.0000 1127.7799
#> [15] 1137.1101 1200.0017 1204.3868 1207.1436 1219.4454 1227.3745 1235.4176
#> [22] 1237.5000 1238.8896 1253.1241 1256.2502 1259.3757

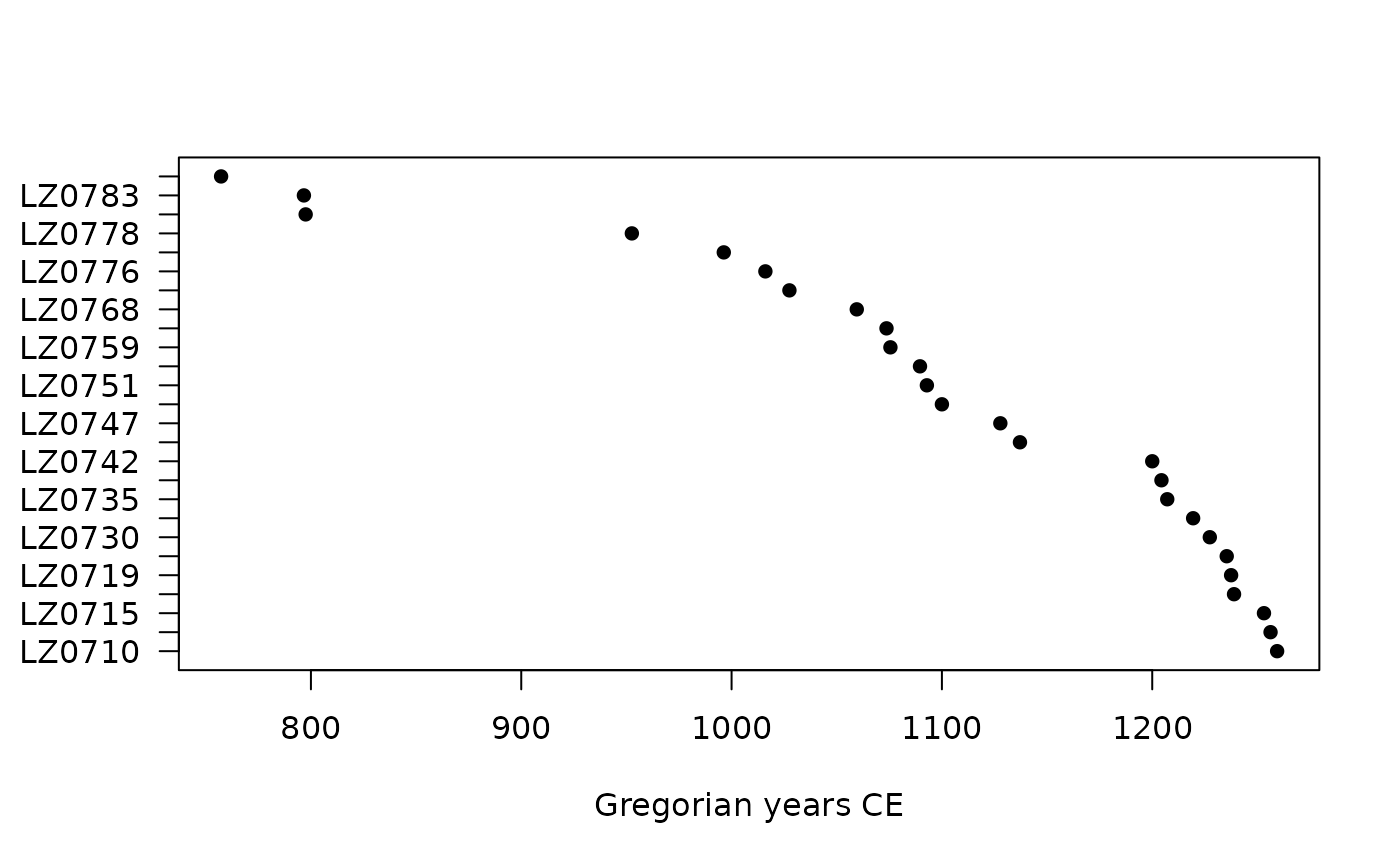
## Plot
plot(mc_dates)


## Bootstrap resampling
boot <- bootstrap(mc_dates, n = 30)
head(boot)
#>         original      mean       bias     error
#> LZ0789  757.2917       NaN        NaN        NA
#> LZ0783  796.6667  858.4295 61.7628395 121.16457
#> LZ0782  797.5000  871.5139 74.0139084  98.12367
#> LZ0778  952.5862  952.3055 -0.2807372 109.08688
#> LZ0777  996.2963 1011.9250 15.6286638  87.38330
#> LZ0776 1016.0714 1012.1865 -3.8849198  75.93731

## Jackknife resampling
jack <- jackknife(mc_dates)
head(jack)
#>         original      mean       bias    error
#> LZ0789  757.2917  768.2870 186.921296 207.5535
#> LZ0783  796.6667  806.9974 175.621693 228.0861
#> LZ0782  797.5000  804.1715 113.415558 169.0563
#> LZ0778  952.5862  954.5205  32.882529 138.6064
#> LZ0777  996.2963  996.6640   6.251785 111.0144
#> LZ0776 1016.0714 1017.1652  18.594831  72.6602

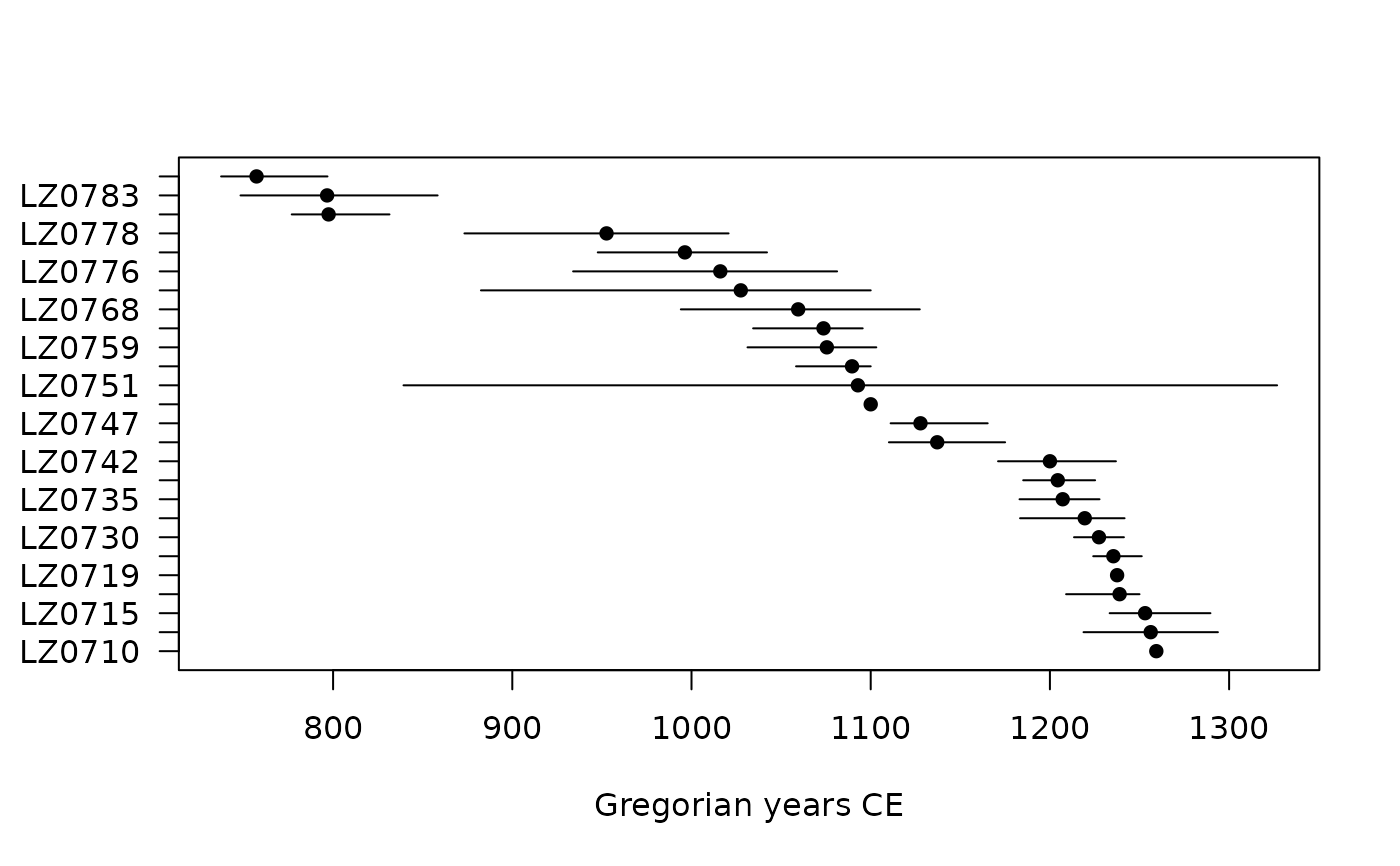
## Simulation
sim <- simulate(mc_dates, nsim = 30)
plot(sim, interval = "range", pch = 16)

Usage

Arguments

Value

See also

Author

Examples