Mean Ceramic Date

Estimates the Mean Ceramic Date of an assemblage.

Usage

mcd(object, dates, ...)

# S4 method for class 'numeric,numeric'
mcd(object, dates, calendar = CE())

# S4 method for class 'data.frame,numeric'
mcd(object, dates, calendar = CE())

# S4 method for class 'matrix,numeric'
mcd(object, dates, calendar = CE())

Arguments

object: A \(m \times p\) numeric matrix or data.frame of count data (absolute frequencies giving the number of individuals for each category, i.e. a contingency table). A data.frame will be coerced to a numeric matrix via data.matrix().
dates: A length-\(p\) numeric vector of dates expressed in years.
...: Currently not used.
calendar: An aion::TimeScale object specifying the calendar of dates (see aion::calendar()). Defaults to Gregorian Common Era.

Value

A MeanDate object.

Details

The Mean Ceramic Date (MCD) is a point estimate of the occupation of an archaeological site (South 1977). The MCD is estimated as the weighted mean of the date midpoints of the ceramic types (based on absolute dates or the known production interval) found in a given assemblage. The weights are the relative frequencies of the respective types in the assemblage.

References

South, S. A. (1977). Method and Theory in Historical Archaeology. New York: Academic Press.

Author

N. Frerebeau

Examples

## Data from Peeples and Schachner 2012
data("zuni", package = "folio")

## Set the start and end dates for each ceramic type
dates <- list(
  LINO = c(600, 875), KIAT = c(850, 950), RED = c(900, 1050),
  GALL = c(1025, 1125), ESC = c(1050, 1150), PUBW = c(1050, 1150),
  RES = c(1000, 1200), TULA = c(1175, 1300), PINE = c(1275, 1350),
  PUBR = c(1000, 1200), WING = c(1100, 1200), WIPO = c(1125, 1225),
  SJ = c(1200, 1300), LSJ = c(1250, 1300), SPR = c(1250, 1300),
  PINER = c(1275, 1325), HESH = c(1275, 1450), KWAK = c(1275, 1450)
)

## Calculate date midpoints
mid <- vapply(X = dates, FUN = mean, FUN.VALUE = numeric(1))

## Calculate MCD
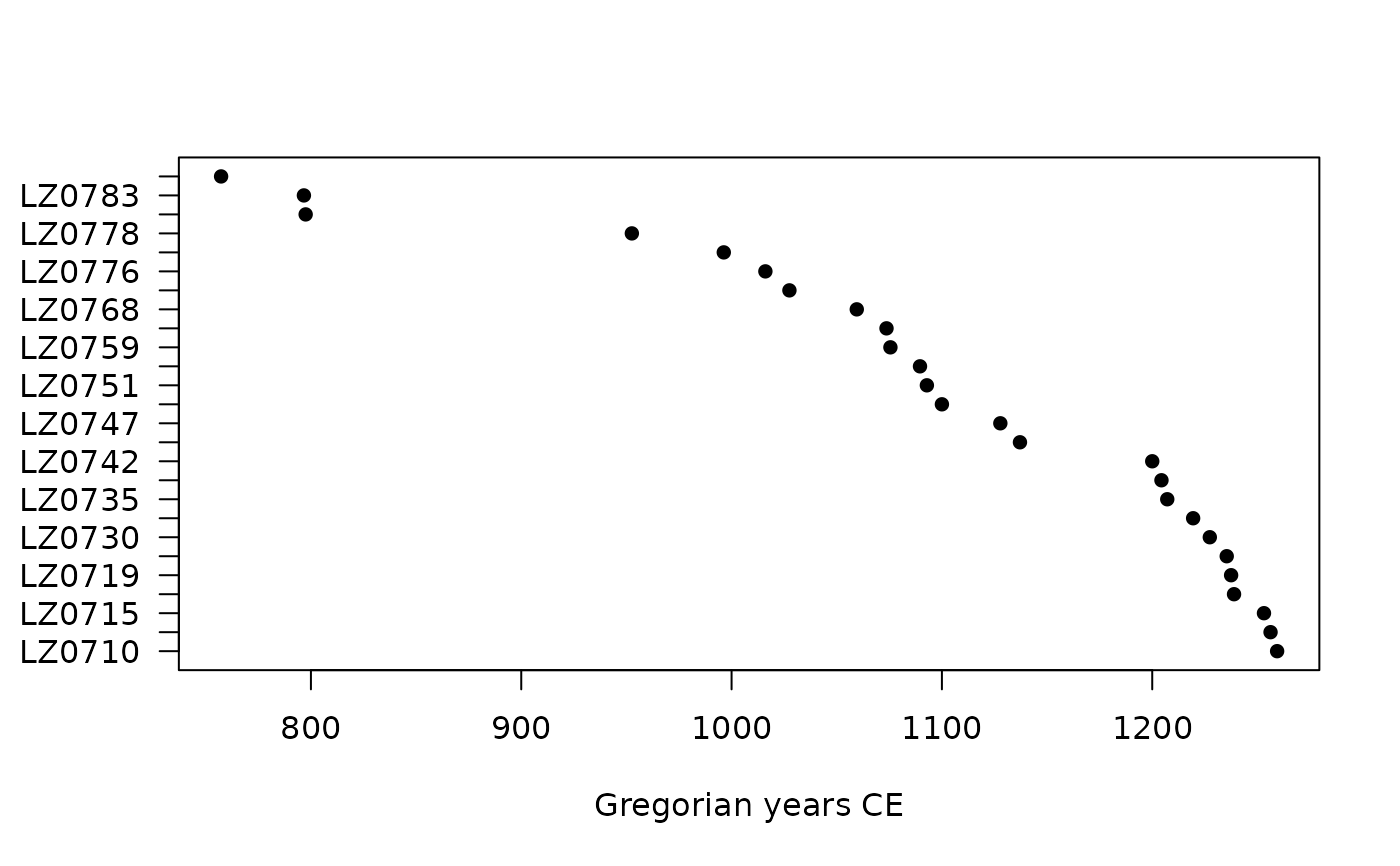
(mc_dates <- mcd(zuni[100:125, ], dates = mid))
#> 26 x 18 x 1 time series observed between 757.291 CE and 1259.38 CE

## Get MCD in years CE
time(mc_dates, calendar = CE())
#>  [1]  757.2912  796.6659  797.4991  952.5855  996.2952 1016.0738 1027.5011
#>  [8] 1059.5249 1073.6597 1075.5213 1089.5820 1092.8564 1100.0000 1127.7799
#> [15] 1137.1101 1200.0017 1204.3868 1207.1436 1219.4454 1227.3745 1235.4176
#> [22] 1237.5000 1238.8896 1253.1241 1256.2502 1259.3757

## Bootstrap resampling
boot <- bootstrap(mc_dates, n = 30)
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
#> Warning: Extreme order statistics used as endpoints.
head(boot)
#>         original      mean      bias    error    lower     upper
#> LZ0789  757.2917  755.6424 -1.649306 14.25382 707.8125  777.0833
#> LZ0783  796.6667  794.1667 -2.500000 31.23112 724.1667  845.0000
#> LZ0782  797.5000  799.9069  2.406863 12.30931 771.7647  826.0294
#> LZ0778  952.5862  956.4943  3.908046 31.53658 896.9828 1007.3276
#> LZ0777  996.2963  997.0833  0.787037 20.73150 953.0093 1040.5093
#> LZ0776 1016.0714 1012.0238 -4.047619 46.18264 933.9286 1133.0357

## Jackknife resampling
jack <- jackknife(mc_dates)
head(jack)
#>         original      mean       bias    error
#> LZ0789  757.2917  768.2870 186.921296 207.5535
#> LZ0783  796.6667  806.9974 175.621693 228.0861
#> LZ0782  797.5000  804.1715 113.415558 169.0563
#> LZ0778  952.5862  954.5205  32.882529 138.6064
#> LZ0777  996.2963  996.6640   6.251785 111.0144
#> LZ0776 1016.0714 1017.1652  18.594831  72.6602

## Plot
plot(mc_dates, decreasing = FALSE)
## Add bootstrap confidence intervals
segments(x0 = boot$lower, y0 = seq_len(nrow(boot)),
         x1 = boot$upper, y1 = seq_len(nrow(boot)))