Skip to contents

Correspondence Analysis

Source: R/AllGenerics.R, R/ca.R
ca.Rd

Computes a simple correspondence analysis based on the singular value decomposition.

Usage

ca(object, ...)

# S4 method for class 'data.frame'
ca(object, rank = NULL, sup_row = NULL, sup_col = NULL)

# S4 method for class 'matrix'
ca(object, rank = NULL, sup_row = NULL, sup_col = NULL)

Arguments

object

A \(m \times p\) numeric matrix or a data.frame.

...

Currently not used.

rank

An integer value specifying the maximal number of components to be kept in the results. If NULL (the default), \(min(m, p) - 1\) components will be returned.

sup_row

A vector specifying the indices of the supplementary rows.

sup_col

A vector specifying the indices of the supplementary columns.

Value

A CA object.

References

Greenacre, M. J. Theory and Applications of Correspondence Analysis. London: Academic Press, 1984.

Greenacre, M. J. Correspondence Analysis in Practice. Seconde edition. Interdisciplinary Statistics Series. Boca Raton: Chapman & Hall/CRC, 2007.

Lebart, L., Piron, M. and Morineau, A. Statistique exploratoire multidimensionnelle: visualisation et inférence en fouille de données. Paris: Dunod, 2006.

See also

svd()

Other multivariate analysis: mca(), pca(), pcoa(), predict()

Author

N. Frerebeau

Examples

## Data from Lebart et al. 2006, p. 170-172
data("colours")

## The chi square of independence between the two variables
stats::chisq.test(colours)
#> 
#> 	Pearson's Chi-squared test
#> 
#> data:  colours
#> X-squared = 138.29, df = 9, p-value < 2.2e-16
#> 

## Compute correspondence analysis
X <- ca(colours)

## Plot rows
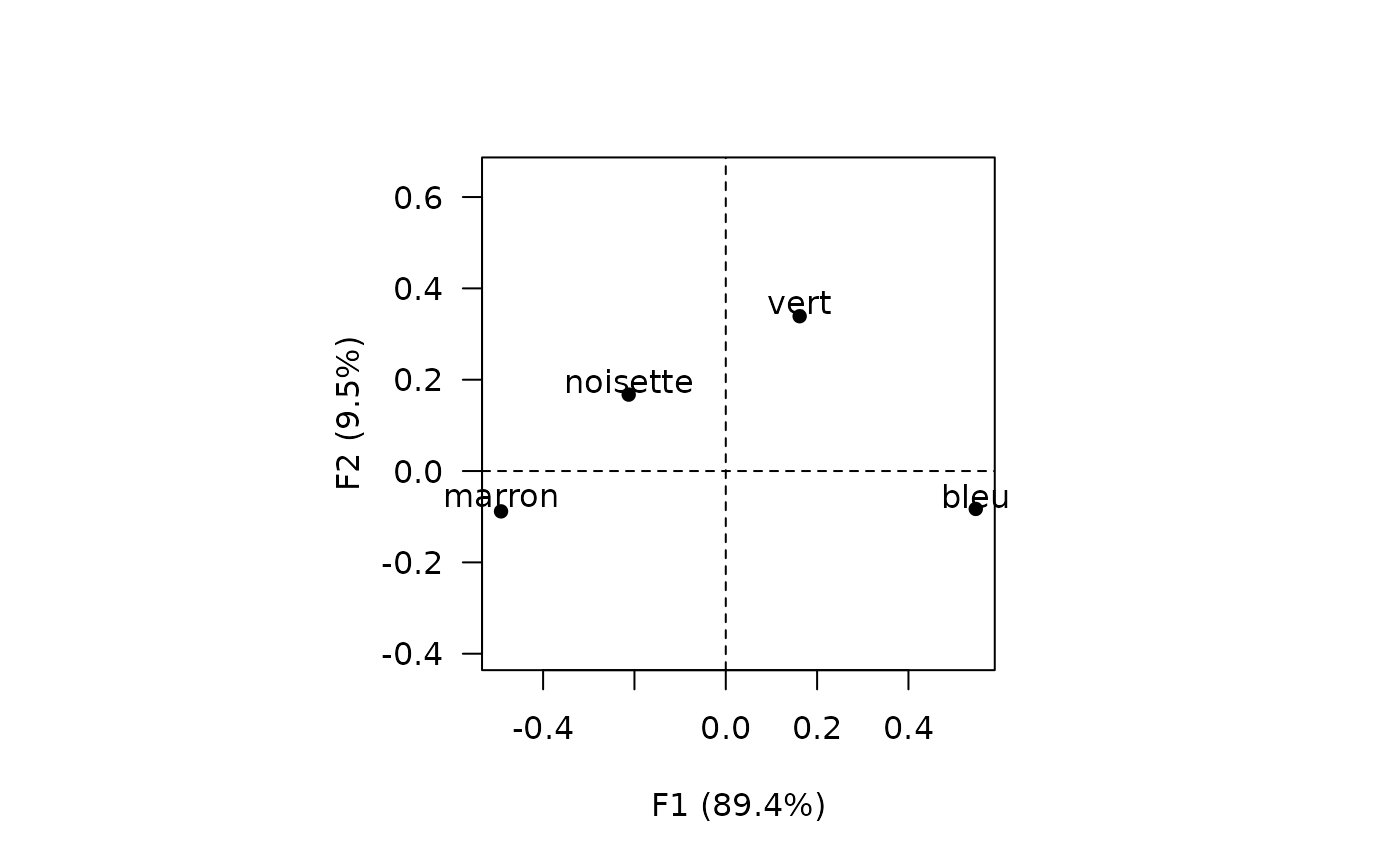
viz_rows(X, labels = TRUE)


## Plot columns
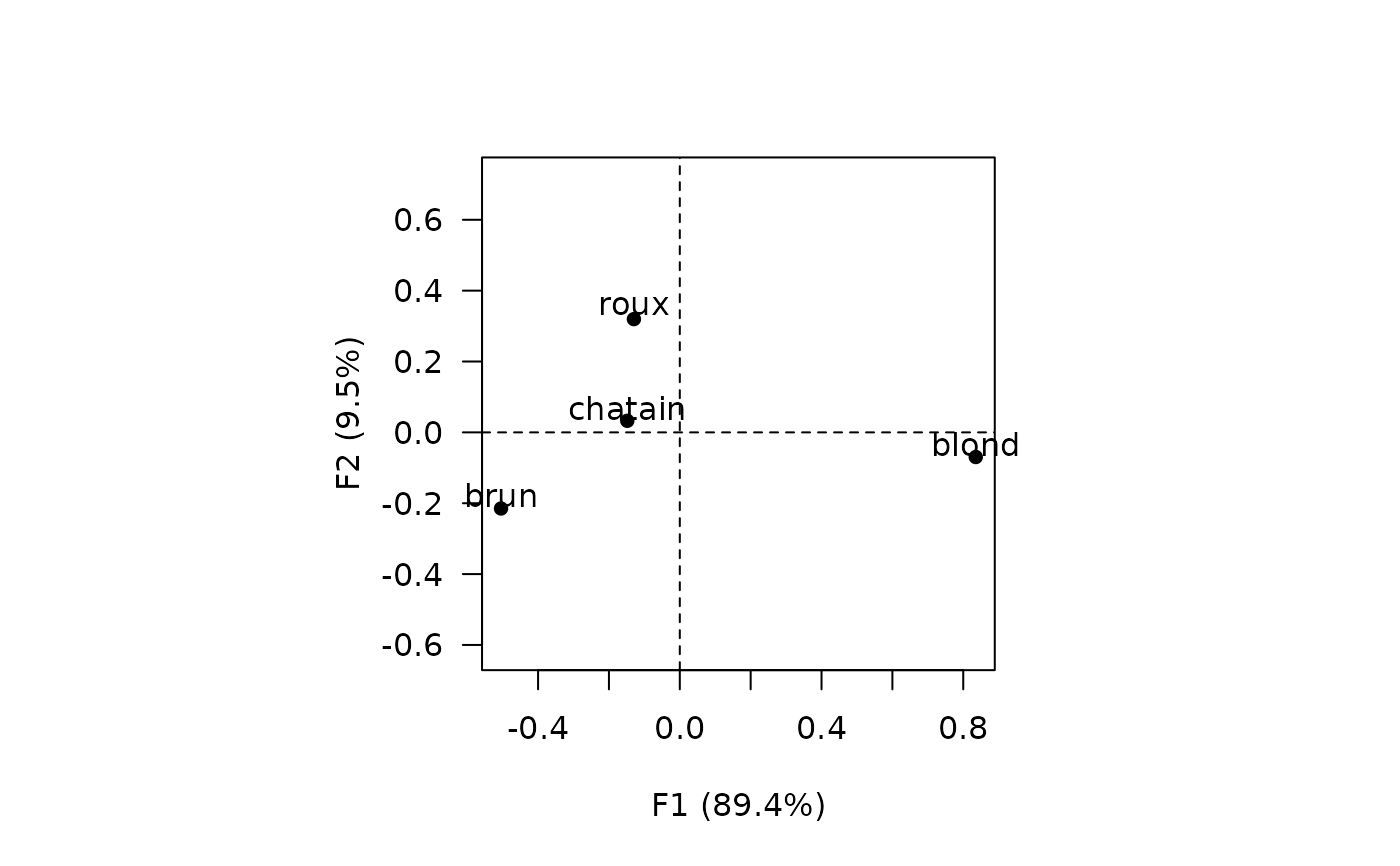
viz_columns(X, labels = TRUE)


## Get row coordinates
get_coordinates(X, margin = 1)
#>                  F1          F2           F3  .sup
#> marron   -0.4921577 -0.08832151  0.021611305 FALSE
#> noisette -0.2125969  0.16739109 -0.100518284 FALSE
#> vert      0.1617534  0.33903957  0.087597437 FALSE
#> bleu      0.5474139 -0.08295428 -0.004709408 FALSE

## Get column coordinates
get_coordinates(X, margin = 2)
#>                 F1          F2          F3  .sup
#> brun    -0.5045624 -0.21482046  0.05550909 FALSE
#> chatain -0.1482527  0.03266635 -0.04880414 FALSE
#> roux    -0.1295233  0.31964240  0.08315117 FALSE
#> blond    0.8353478 -0.06957934  0.01621471 FALSE

## Get total inertia
sum(get_inertia(X))
#> [1] 0.2335977

## Get row contributions
get_contributions(X, margin = 1)
#>                 F1       F2         F3
#> marron   43.115744 13.04249  6.6795992
#> noisette  3.400961 19.80398 61.0855951
#> vert      1.354851 55.90952 31.9248234
#> bleu     52.128445 11.24401  0.3099822