Outlier Detection

Usage

detect_outlier(object, reference, ...)

is_outlier(object, ...)

# S4 method for class 'CompositionMatrix,missing'
detect_outlier(
  object,
  ...,
  robust = TRUE,
  method = c("mve", "mcd"),
  quantile = 0.975
)

# S4 method for class 'CompositionMatrix,CompositionMatrix'
detect_outlier(
  object,
  reference,
  ...,
  robust = TRUE,
  method = c("mve", "mcd"),
  quantile = 0.975
)

# S4 method for class 'OutlierIndex'
is_outlier(object, robust = TRUE)

Arguments

object: A CompositionMatrix.
reference: A CompositionMatrix. If missing, object is used.
...: Further parameters to be passed to MASS::cov.rob().
robust: A logical scalar: should robust estimators be used?
method: A character string specifying the method to be used. It must be one of "mve" (minimum volume ellipsoid) or "mcd" (minimum covariance determinant; see MASS::cov.rob()). Only used if robust is TRUE.
quantile: A length-one numeric vector giving the significance level. quantile is used as a cut-off value for outlier detection: observations with larger (squared) Mahalanobis distance are considered as potential outliers.

Value

detect_outlier() returns an OutlierIndex object.
is_outlier() returns a logical vector.

Details

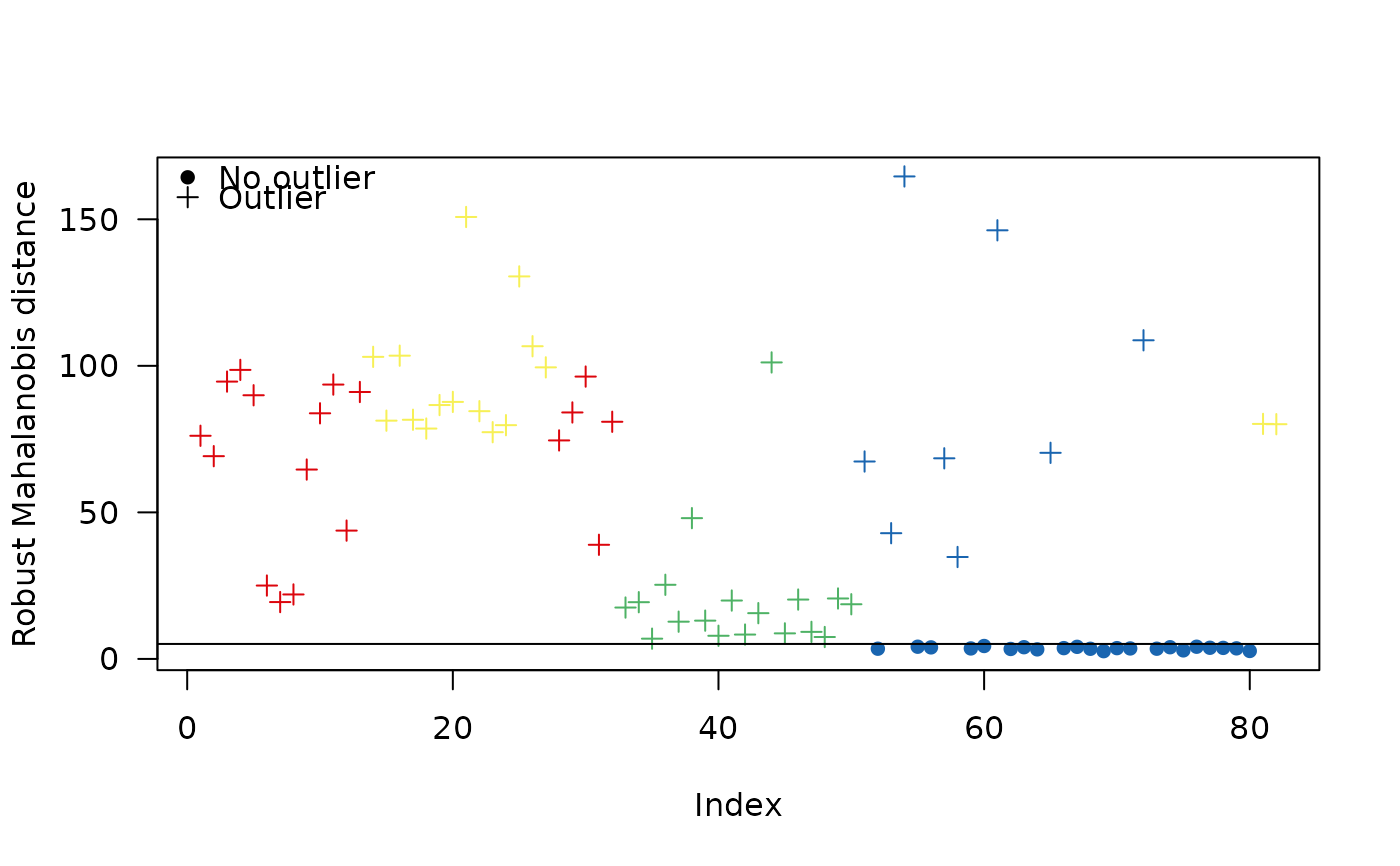
An outlier can be defined as having a very large Mahalanobis distance from all observations. In this way, a certain proportion of the observations can be identified, e.g. the top 2% of values (i.e. values above the 0.98th percentile of the Chi-2 distribution).

On the one hand, the Mahalanobis distance is likely to be strongly affected by the presence of outliers. Rousseeuw and van Zomeren (1990) thus recommend using robust methods (which are not excessively affected by the presence of outliers).

On the other hand, the choice of the threshold for classifying an observation as an outlier should be discussed. There is no apparent reason why a particular threshold should be applicable to all data sets (Filzmoser, Garrett, and Reimann 2005).

References

Filzmoser, P., Garrett, R. G. & Reimann, C. (2005). Multivariate outlier detection in exploration geochemistry. Computers & Geosciences, 31(5), 579-587. doi:10.1016/j.cageo.2004.11.013 .

Filzmoser, P. & Hron, K. (2008). Outlier Detection for Compositional Data Using Robust Methods. Mathematical Geosciences, 40(3), 233-248. doi:10.1007/s11004-007-9141-5 .

Filzmoser, P., Hron, K. & Reimann, C. (2012). Interpretation of multivariate outliers for compositional data. Computers & Geosciences, 39, 77-85. doi:10.1016/j.cageo.2011.06.014 .

Rousseeuw, P. J. & van Zomeren, B. C. (1990). Unmasking Multivariate Outliers and Leverage Points. Journal of the American Statistical Association, 85(411): 633-639. doi:10.1080/01621459.1990.10474920 .

Santos, F. (2020). Modern methods for old data: An overview of some robust methods for outliers detection with applications in osteology. Journal of Archaeological Science: Reports, 32, 102423. doi:10.1016/j.jasrep.2020.102423 .

Author

N. Frerebeau

Examples

## Data from Day et al. 2011
data("kommos", package = "folio") # Coerce to compositional data
kommos <- remove_NA(kommos, margin = 1) # Remove cases with missing values
coda <- as_composition(kommos, parts = 3:17, groups = 1)

## Detect outliers
out <- detect_outlier(coda)

plot(out, type = "dotchart")

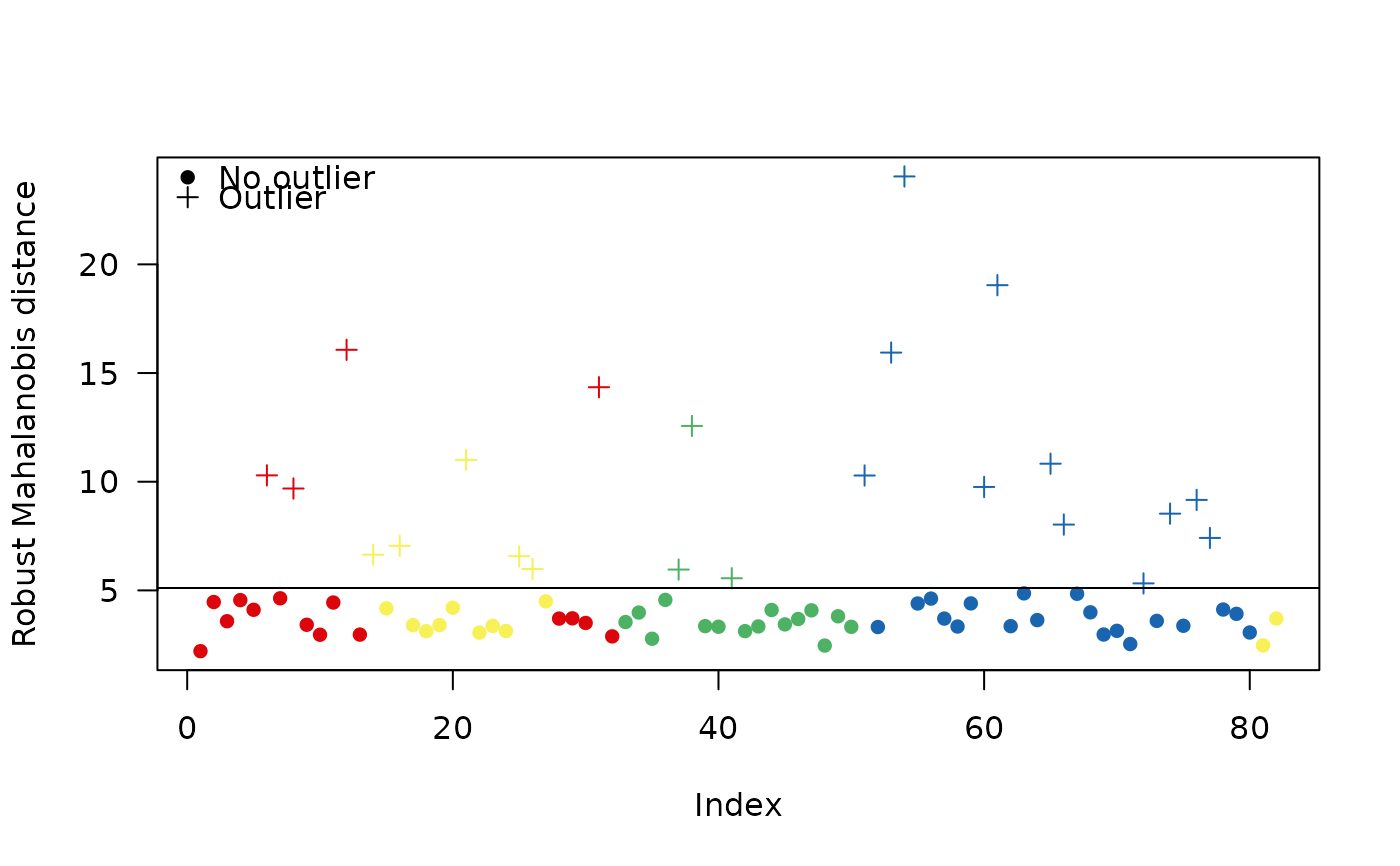plot(out, type = "distance")


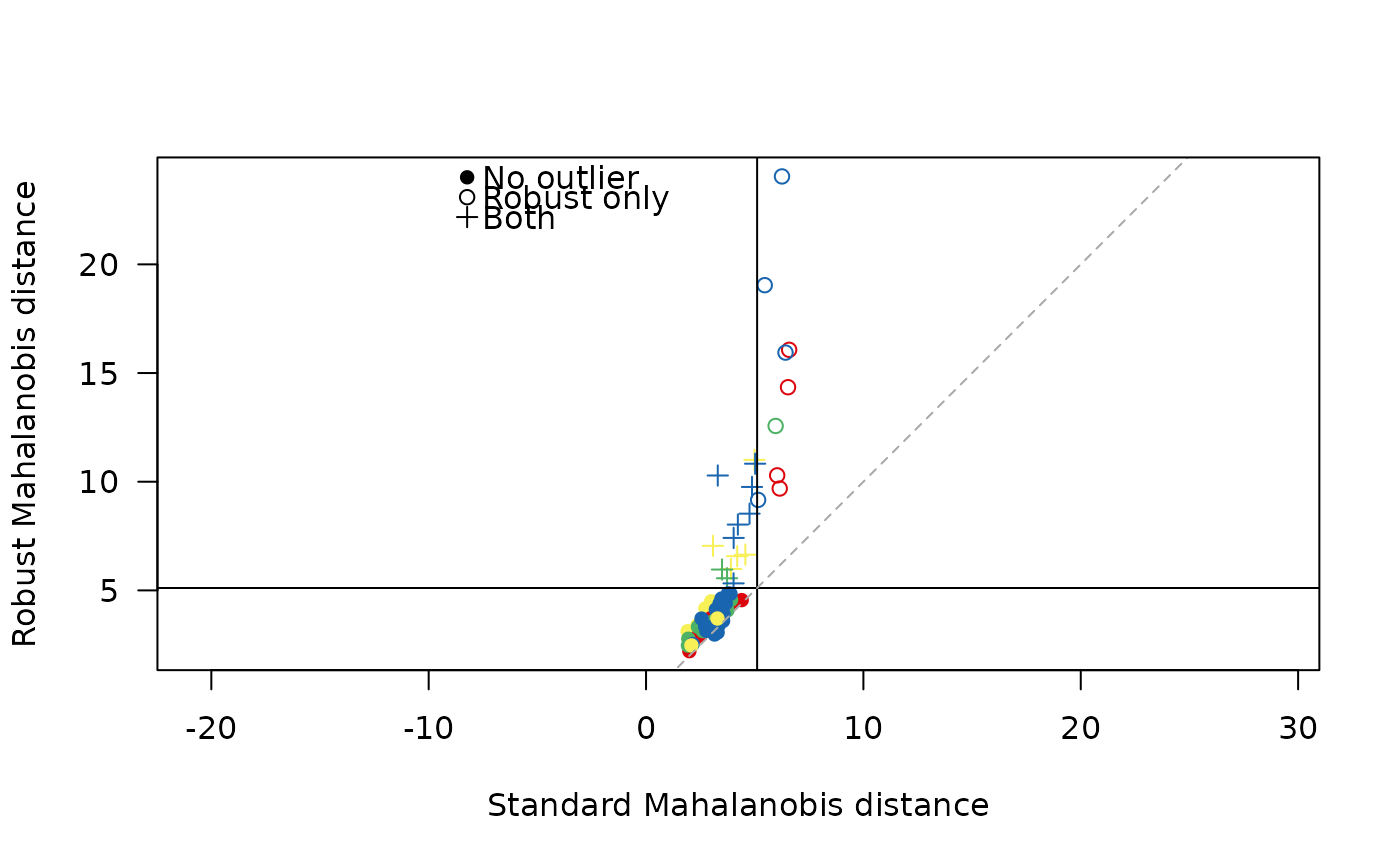## Detect outliers according to CJ
ref <- extract(coda, "CJ")
out <- detect_outlier(coda, reference = ref, method = "mcd")
plot(out, type = "dotchart")